2阶系统,什么是2阶系统？

什么是2阶系统？

在系统理论中，2阶系统是一个重要的概念，它描述了一个动态系统的行为，其中系统不仅受到其当前状态的影响，还受到其历史状态的影响。这种反馈机制使得2阶系统在许多领域，如物理学、生物学、经济学和社会科学中，具有广泛的应用。

2阶系统的特点

2阶系统的主要特点包括：

状态依赖：系统的当前状态不仅取决于当前输入，还取决于过去的状态。

历史依赖：系统的行为受到历史状态的影响，这意味着系统的未来状态与过去的状态密切相关。

非线性：2阶系统通常表现出非线性动态，这意味着系统的输出与输入之间的关系不是简单的线性关系。

2阶系统的分类

根据系统响应的稳定性，可以分为稳定系统和不稳定系统。

根据系统内部反馈的强度，可以分为弱反馈系统和强反馈系统。

根据系统响应的时间特性，可以分为快速响应系统和慢速响应系统。

2阶系统的应用实例

2阶系统在各个领域的应用实例包括：

物理学：在量子力学中，2阶系统可以用来描述粒子的行为，如电子在原子中的运动。

生物学：在生态系统中，2阶系统可以用来模拟物种之间的相互作用，如捕食者与猎物之间的关系。

经济学：在金融市场分析中，2阶系统可以用来预测股票价格的变化，考虑历史价格趋势和交易量。

社会科学：在社会网络分析中，2阶系统可以用来研究个体之间的互动，如朋友关系和社交网络的形成。

2阶系统的建模与仿真

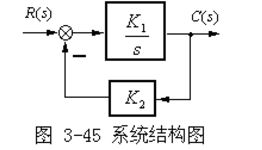
微分方程：使用微分方程来描述系统的动态行为，可以捕捉到系统状态随时间的变化。

差分方程：当系统的时间尺度较大时，可以使用差分方程来近似描述系统的行为。

离散事件模拟：对于离散事件驱动的系统，可以使用离散事件模拟来研究系统的行为。

2阶系统的挑战与展望

尽管2阶系统在理论和应用上具有重要意义，但在实际研究中仍面临一些挑战：

复杂性：2阶系统的非线性特性使得系统行为复杂，难以精确预测。

数据需求：为了建立准确的模型，需要大量的历史数据。

参数估计：系统参数的估计可能存在不确定性，影响模型的准确性。

未来，随着计算能力的提升和数据分析技术的进步，2阶系统的建模和仿真将更加精确，为各个领域的研究提供更强大的工具。

2阶系统是一个描述动态系统行为的理论框架，它在多个领域有着广泛的应用。通过理解2阶系统的特点、分类、应用实例以及建模与仿真方法，我们可以更好地把握系统的动态行为，为解决实际问题提供理论支持。