b进制系统,b进制系统的定义

进制系统是数学和计算机科学中不可或缺的概念，它定义了数字的表示和计算方式。常见的进制系统包括十进制、二进制和十六进制等。本文将探讨一种特殊的进制系统——b进制系统，并分析其特点和应用。

b进制系统的定义

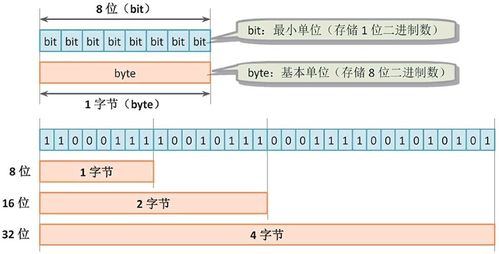
b进制系统是一种以b为底数的进制系统，其中b是一个正整数。在这种系统中，数字的每一位都可以取从0到b-1的任意值。例如，十进制系统可以看作是10进制系统，而二进制系统则是2进制系统。

b进制系统的表示方法

b进制系统的表示方法与十进制系统类似，但每一位的取值范围不同。例如，一个三位b进制数可以表示为：

abc_b = a b^2 + b b^1 + c b^0

其中，a、b、c分别代表该b进制数的百位、十位和个位数字，且它们的取值范围均为0到b-1。

b进制系统的转换方法

将b进制数转换为十进制数的方法与十进制数转换为b进制数的方法类似。以下是两种转换方法的步骤：

将b进制数转换为十进制数

从右到左，将每一位数字乘以其对应的b的幂次。

将所有乘积相加，得到十进制数。

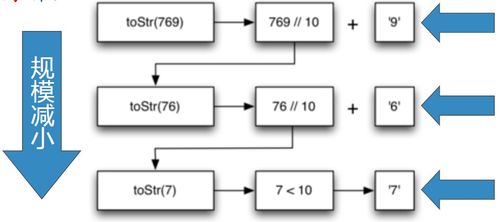
将十进制数转换为b进制数

将十进制数除以b，得到商和余数。

将余数作为b进制数的最低位。

将商再次除以b，重复步骤1和2，直到商为0。

将所有余数从下到上排列，得到b进制数。

b进制系统的应用

计算机科学

二进制系统是计算机硬件和软件的基础，因为计算机使用二进制数来表示和处理数据。

十六进制系统常用于表示内存地址和颜色代码，因为它可以更直观地表示二进制数。

数学

b进制系统可以用于研究数论和组合数学中的问题。

在密码学中，b进制系统可以用于加密和解密信息。

b进制系统的优势与局限性

b进制系统具有以下优势：

简洁性：b进制系统可以更简洁地表示数字，尤其是在b较小的情况下。

直观性：在某些情况下，b进制系统可以更直观地表示数字之间的关系。

b进制系统也存在以下局限性：

复杂性：当b较大时，b进制系统的表示和转换可能会变得复杂。

兼容性：在某些应用场景中，b进制系统可能与现有的系统不兼容。

结论

b进制系统是一种有趣的进制系统，它在计算机科学和数学中有着广泛的应用。尽管b进制系统存在一些局限性，但它在特定场景下仍然具有优势。通过了解b进制系统的定义、表示方法、转换方法和应用，我们可以更好地理解进制系统的本质，并在实际应用中发挥其作用。