1阶系统,什么是一阶系统什么是二阶系统

一阶系统的概述

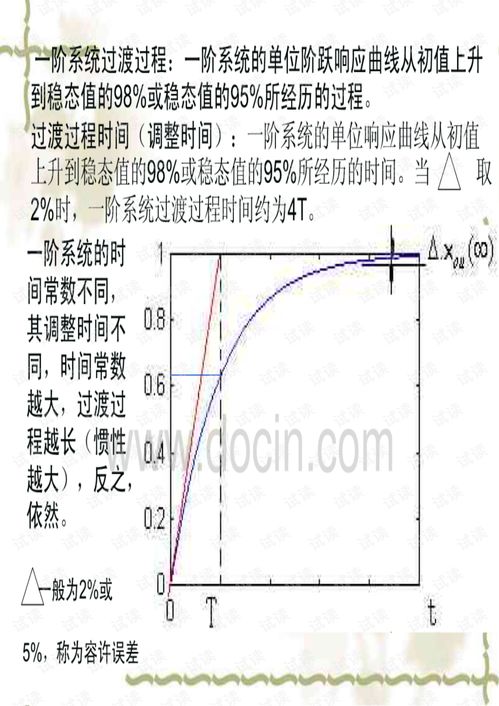
一阶系统是自动控制理论中的一个基本概念，指的是系统中的微分方程的最高阶数为1的系统。这类系统在工程和科学研究中非常常见，因为许多实际系统都可以简化为一阶系统。一阶系统通常具有简单的动态特性，便于分析和设计。

一阶系统的数学模型

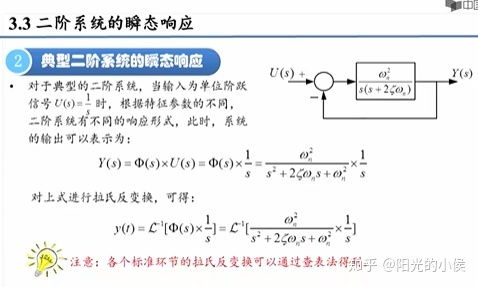
一阶系统的数学模型通常由一阶线性微分方程描述。其一般形式为：( frac{dx}{dt} = ax + b )，其中( x(t) )是系统的状态变量，( a )和( b )是常数。这个方程表示系统的状态变量随时间的变化率与当前状态值成正比，并可能受到一个常数输入的影响。

一阶系统的时域分析

时域分析是研究系统动态特性的基本方法之一。对于一阶系统，时域分析主要包括以下内容：

零输入响应：系统在没有外部输入的情况下，仅由初始条件引起的响应。

零状态响应：系统在初始状态为零的情况下，由外部输入引起的响应。

阶跃响应：系统在单位阶跃输入下的响应，是分析系统动态性能的重要指标。

一阶系统的阶跃响应

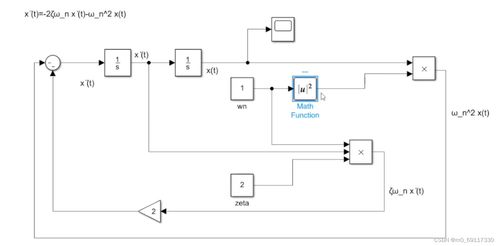
阶跃响应是指系统在单位阶跃输入下的响应。对于一阶系统，阶跃响应具有以下特点：

上升时间：系统输出从10%上升到90%所需的时间。

峰值时间：系统输出达到峰值所需的时间。

超调量：系统输出峰值与稳态值之差与稳态值之比。

调节时间：系统输出进入并保持在稳态值±2%范围内的时间。

一阶系统的传递函数

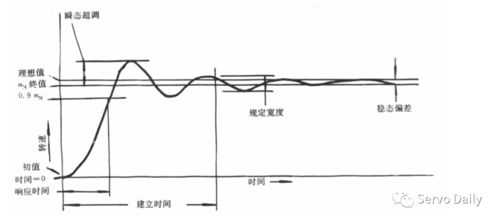
传递函数是描述系统动态特性的另一种方法。对于一阶系统，其传递函数可以表示为：( G(s) = frac{a}{s + frac{1}{a}} )，其中( s )是拉普拉斯变换中的复变量。传递函数可以用于分析系统的频率响应和稳定性。

一阶系统的稳定性分析

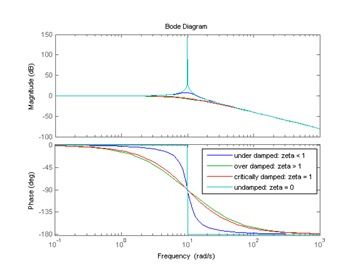
稳定性是一阶系统设计中的重要指标。根据传递函数，可以判断一阶系统的稳定性。如果传递函数的极点位于复平面的左半平面，则系统是稳定的；如果极点位于右半平面，则系统是不稳定的。

一阶系统的应用

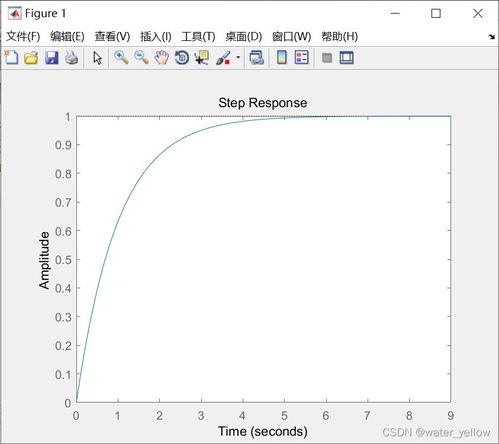
电路系统：如RC电路、RL电路等。

控制系统：如PID控制器、滤波器等。

生物系统：如药物在体内的代谢过程、酶促反应等。

经济系统：如投资回报、经济增长等。

一阶系统是自动控制理论中的一个基本概念，具有简单的动态特性。通过对一阶系统的数学模型、时域分析、传递函数和稳定性分析等方面的研究，可以更好地理解和设计实际系统。一阶系统在工程和科学研究中具有广泛的应用，对于提高系统性能和优化设计具有重要意义。